Площадь фигуры вращения вокруг ох. Нахождение площади поверхности тел вращения. Приложения определенного интеграла к решению некоторых задач механики и физики

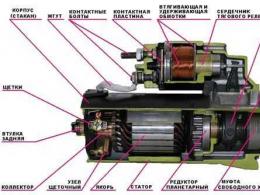
Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой поверхности вращения. Поверхность вращения, или, что то же самое - поверхность тела вращения - пространственная фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).

Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой. Тело, образованное вращением этой трапеции вокруг то же оси Ox , и есть тело вращения. А площадь поверхности вращения или поверхности тела вращения - это его внешняя оболочка, не считая кругов, образованных вращением вокруг оси прямых x = a и x = b .

Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox , а вокруг оси Oy .

Вычисление площади поверхности вращения, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f (x ) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a .

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:

Ответ: длина дуги кривой равна

.

Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .

Решение. Достаточно вычислить площадь поверхности, получающейся от вращения одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности вращения:

.

Производим интегрирование от 0 до a :

Вычисление площади поверхности вращения, заданной параметрически

Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями

Тогда площадь поверхности вращения вычисляется по формуле

(2).

Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a . Циклоида задана параметрическими уравнениями

Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a , найдём

Из этого следует, что границы интегрирования соответствуют

Теперь можем применить формулу (2). Найдём производные:

Запишем подкоренное выражение в формуле, подставляя найденные производные:

Найдём корень из этого выражения:

.

Подставим найденное в формулу (2):

.

Произведём подстановку:

И, наконец, находим

В преобразовании выражений были использованы тригонометрические формулы

Ответ: площадь поверхности вращения равна .

Вычисление площади поверхности вращения, заданной в полярных координатах

Пусть кривая, вращением которой образована поверхность, задана в полярных координатах.

Приветствую вас, уважаемые студенты вуза Аргемоны!

Сегодня мы продолжим учиться материализации предметов. В прошлый раз мы вращали плоские фигуры и получали объёмные тела. Некоторые из них - очень даже заманчивые и полезные. Думаю, что многому, что изобретает маг, можно в дальнейшем найти применение.

Сегодня мы будет вращать кривые. Понятно, что таким образом мы можем получить какой-то предмет с очень тонкими гранями (колбочка или флакон для зелий, ваза для цветов, стакан для напитков и т.п.), потому как вращающаяся кривая именно такого рода предметы и может сотворить. Другими словами, вращением кривой мы можем получить какую-то поверхность - замкнутую со всех сторон или нет. Почему прямо сейчас вспомнилась дырявая чаша, из которой всё время пил сэр Шурф Лонли-Локли.

Вот мы и сотворим дырявую чашу и недырявую, и подсчитаем площадь сотворённой поверхности. Думаю, для чего-то она (вообще площадь поверхности) ведь будет нужна - ну хотя бы для нанесения специальной магической краски. А с другой стороны, площади магических артефактов могут потребоваться для расчёта приложенных к ним магических сил или ещё чего-то. Мы научимся это находить, а уж где применить - найдём.

Итак, форму чаши вполне нам может дать кусок параболы. Возьмём самую простейшую y=x 2 на промежутке . Видно, что при вращении её вокруг оси OY получается как раз чаша. Без дна.

Заклинание для расчёта площади поверхности вращения выглядит следующим образом:

Здесь |y| - это расстояние от оси вращения до любой точки кривой, которая вращается. Как известно, расстояние - это перпендикуляр.
Немного труднее со вторым элементом заклинания: ds - это дифференциал дуги. Эти слова нам ничего не дают, поэтому не будем заморачиваться, а перейдём на язык формул, где этот дифференциал явно представлен для всех известных нам случаев:
- декартовой системы координат;
- записи кривой в параметрическом виде;
- полярной системы координат.

Для нашего случая расстояние от оси вращения до любой точки на кривой равно х. Считаем площадь поверхности получившейся дырявой чаши:

Чтобы сделать чашу с дном, нужно взять ещё кусочек, но другой кривой: на интервале это линия y=1.

Ясно, что при её вращении вокруг оси OY получится донышко чаши в виде круга единичного радиуса. И мы знаем, как считается площадь круга (по формуле пи*r^2. Для нашего случая площадь круга будет равна пи), но вычислим его по новой формуле - для проверки.
Расстояние от оси вращения до любой точки этого кусочка кривой также равно х.

Ну вот, расчёты наши верны, что радует.

А теперь домашнее задание .

1. Найти площадь поверхности, полученной вращением ломаной ABC, где A=(1; 5), B=(1; 2), C=(6; 2), вокруг оси ОХ.
Совет. Записать все отрезки в параметрическом виде.
AB: x=1, y=t, 2≤t≤5
BC: x=t, y=2, 1≤t≤6
Кстати, на что похож получившийся предмет?

2. Ну а теперь придумайте что-то сами. Трёх предметов, думаю, хватит.

Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными осии проходящими через точкиx
на ней. Площадь фигуры, образующейся в сечении, зависит от точки х , определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на функцией. Тогда объем части тела, находящейся между плоскостямих=а и х=в вычисляется по формуле

Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса :, горизонтальной плоскостьюи наклонной плоскостьюz=2y и лежащего выше горизонтальной плоскости .

Очевидно, что рассматриваемое тело проектируется на осьв отрезок
, а приx
поперечное сечение тела представляет собою прямоугольный треугольник с катетамиy и z=2y, где y можно выразить через x из уравнения цилиндра:

Поэтому площадь S(x) поперечного сечения такова:

Применяя формулу, находим объём тела :

Вычисление объемов тел вращения

Пусть на отрезке[a , b ] задана непрерывная знакопостоянная функция y = f (x ). Объемы тела вращения, образованного вращением вокруг оси Ох (или оси Оу ) криволинейной трапеции, ограниченной кривой y = f (x ) (f (x )0) и прямыми у=0, х=а, х= b , вычисляются соответственно по формулам:

, (19)

(20)

Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривой
и прямымиx =0, y = c , y = d , то объем тела вращения равен

. (21)

Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг осиОх .

По формуле (19) искомый объем

Пример. Пусть в плоскости xOy рассматривается линия y=cosx на отрезке .

Эта линия вращается в пространстве вокруг оси, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объёмэтого тела вращения.

Согласно формуле, получаем:

Площадь поверхности вращения

,
, вращается вокруг осиOx, то площадь поверхности вращения вычисляется по формуле
, гдеa и b - абсциссы начала и конца дуги.

Если дуга кривой, заданная неотрицательной функцией
,
, вращается вокруг осиOy, то площадь поверхности вращения вычисляется по формуле

,

где с и d - абсциссы начала и конца дуги.

Если дуга кривой задана параметрическими уравнениями
,
, причем
, то

Если дуга задана в полярных координатах
, то

.

Пример. Вычислим площадь поверхности, образованной вращением в пространстве вокруг оси части линииy=, расположенной над отрезкомоси.

Так как
, то формула даёт нам интеграл

Сделаем в последнем интеграле замену t=x+(1/2) и получим:

В первом из интегралов правой части сделаем замену z=t 2 -:

Для вычисления второго из интегралов в правой части обозначим его и проинтегрируем по частям, получив уравнение для:

Перенося в левую часть и деля на 2, получаем

откуда, наконец,

Приложения определенного интеграла к решению некоторых задач механики и физики

Работа переменной силы. Рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f , зависящей от положения точки x на оси, т.e. силы, являющейся функцией x . Тогда работа A , необходимая для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:

Для вычисления силы давления жидкости используют закон Паскаля, согласно которому давление жидкости на площадку равно ее площади S , умноженной на глубину погружения h , на плотность ρ и ускорение силы тяжести g , т.е.

.

1. Моменты и центры масс плоских кривых . Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность
, тостатические моменты этой дуги M x и M y относительно координатных осей Ox и Oy равны

;

моменты инерции I Х и I у относительно тех же осей Ох и Оу вычисляются по формулам

а координаты центра масс и- по формулам

где l- масса дуги, т. е.

Пример 1 . Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1.

Если плотность не указана, предполагается, что кривая однородна и
. Имеем:Следовательно,

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти. Имеем:

Отсюда получаем:

В приложениях часто оказывается полезной следующая Теорема Гульдена . Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Пример 3. Найти координаты центра масс полуокружности

Вследствие симметрии
. При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна, а длина полуокружности равна па. По теореме Гульдена имеем 4

Отсюда
, т.е. центр масс C имеет координаты C
.

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах.

Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Так как путь, пройденный телом со скоростью v(t) за отрезок времени , выражается интегралом

то имеем:

П
ример. Найдём площадь ограниченной области, лежащей между осьюи линиейy=x 3 -x. Поскольку

линия пересекает ось в трёх точка:x 1 =-1, x 2 =0, x 3 =1.

Ограниченная область между линией и осью проектируется на отрезок
,причём на отрезке
,линияy=x 3 -x идёт выше оси (то есть линииy=0, а на - ниже. Поэтому площадь области можно подсчитать так:

П
ример. Найдём площадь области, заключённой между первым и вторым витком спирали Архимедаr=a (a>0) и отрезком горизонтальной оси
.

Первый виток спирали соответствует изменению угла в пределах от 0 до, а второй - отдо. Чтобы привести изменение аргументак одному промежутку, запишем уравнение второго витка спирали в виде
,

. Тогда площадь можно будет найти по формуле, положив
и
:

Пример. Найдём объём тела, ограниченного поверхностью вращения линииy=4x-x 2 вокруг оси (при
).

Для вычисления объёма тела вращения применим формулу

Пример. Вычислим длину дуги линииy=lncosx, расположенной между прямыми и
.

(мы взяли в качестве значения корня , а не -cosx, поскольку cosx >0 при
, длина дуги равна

Ответ:
.

Пример. Вычислим площадь Q поверхности вращения, полученной при вращении дуги циклоиды x=t-sint ; y=1-cost, при

, вокруг оси.

Для вычисления применим формулу:

Имеем:

, так что

Для перехода под знаком интеграла к переменной заметим, что при

получаем

, а также

Кроме того, предварительно вычислим

(так что
) и

Получаем:

Делая замену , приходим к интегралу

Пример: Найти объем шара радиуса R .

В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле .

Тогда функция площадей сечений имеет вид: Q (x ) = .

Получаем объем шара:

Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S .

При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x / H , где х - расстояние от плоскости сечения до вершины пирамиды.

Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.

Отсюда получаем функцию площадей сечений:

Находим объем пирамиды:

Объем тел вращения.

Рассмотрим кривую, заданную уравнением y = f (x ). Предположим, что функция f (x ) непрерывна на отрезке [ a , b ]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемоетело вращения .

y = f (x )

Площадь поверхности тела вращения.

М i B

Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу АВ на n частей точками M 0 , M 1 , M 2 , … , M n . Координаты вершин полученной ломаной имеют координаты x i и y i . При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна D P i . Эта площадь может быть найдена по формуле :